수학] 적분 정적분 부정적분 구하기, 그래프 그리기; 매스매티카 Mathematica Integrate, Integral

매스매티카에서 적분을 하려면 Integrate 함수를 사용합니다. 철자에 주의해야 합니다. Integral (인테그랄) 이 아니라 Integrate 입니다.

예를 들어 x³ 이라는 간단한 3차함수의 적분을 구하려면 다음과 같이 합니다.

* 정적분(Definite Integral) 구하기
Integrate[x^3, {x, 0, 3}]
구간 a, b 를 0, 3 으로 지정했습니다. 답은 "81/4" 즉 "4분의 81"이라는 면적이 나옵니다.


* 부정적분(Indefinite Integral) 구하기
Integrate[x^3, x]
위의 수식을 입력하면

4분의 x⁴ 이라는 F(x) 함수가 출력됩니다. 3차함수의 부정적분을 구하면 즉, 역미분하면 4차함수가 나옵니다.


* 정적분이란, 정해진 구간에서, 함수 f(x)와 x축 사이의 면적을 구하는 것입니다. 아래 그래프에서 색깔이 칠해진 부분의 면적인데, 다만 x축 아래쪽의 빨간 면적은 마이너스가 됩니다.

* 부정적분이란, 주어진 함수 f(x)에서, 대문자 F(x)를 구하는 것입니다. 대문자 F(x)를 미분하면 f(x)가 나옵니다. 따라서 f(x)를 역미분한 것이 대문자 F(x)입니다.

아래 그래프에서 소문자 f(x)는 3차함수인데, 이 3차함수를 도함수로 삼는 함수라면 4차함수일 것입니다. 아래 그래프에서 회색 선이 4차함수인 대문자 F(x)의 그래프입니다. 즉 부정적분의 결과를 그래프로 그린 것입니다.

클릭하면확대

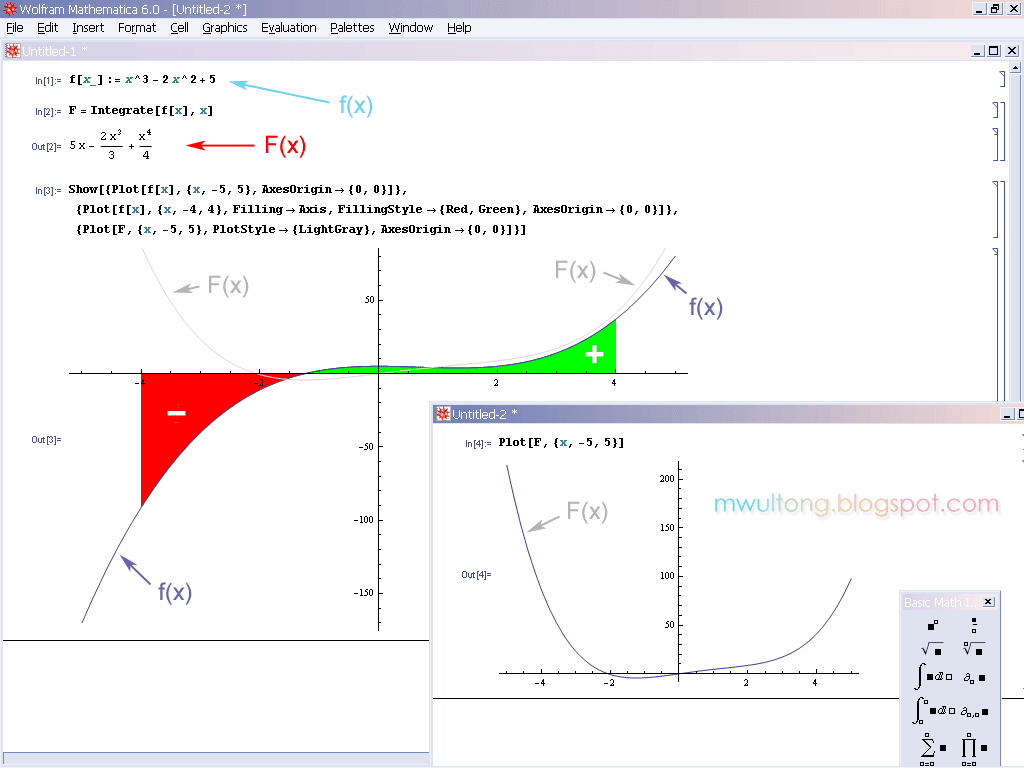
3차함수의 정적분 부정적분 그래프 그리기

위의 그림에서 빠졌는데, 위의 그림 속의 삼차함수의 정적분을 -4, 4 구간에서
Integrate[x^3 - 2 x^2 + 5, {x, -4, 4}]
이렇게 구하면 "-136/3" 이라는 면적이 나옵니다. "-(3분의 136)"입니다. 근사값은 약 -45.33333... 입니다.


아래 코드를 매스매티카 노트북 문서에 입력하고 키패드의 Enter키를 치면, 위의 그림과 같은 결과가 나옵니다.

아래 코드에서 "-5, 5"라는 범위는 전체 그래프를 그릴 x의 범위이고, "-4, 4"는 정적분을 구할 구간입니다.



Show 명령어를 사용하여, 여러 개의 그래프들을 하나로 합쳐 주었습니다.



수학 미분 그래프 그리기 예제: ▶▶ 미분 N계 도함수 구하기, 3차함수 그래프 그리기; 매스매티카 Mathematica Derivative 예제